Introduction
LZW (Lempel-Ziv-Welch) coding is a dictionary-based compression technique, meaning it compresses data by replacing sequences of characters with shorter codes based on a dynamically generated dictionary. It is widely used in lossless compression and is especially popular with efficiency and simplicity.
History
The name LZW comes from the initials of the three creators of the algorithm: Abraham Lempel, Jacob Ziv and Terry Welch. Lempel and Ziv were the original creators of the Lempel-Ziv algorithms, first introduced in the late 1970s. These algorithms laid the foundation for many dictionary-based compression techniques. Terry Welch built upon their work and modified the Lempel-Ziv algorithm in 1984, resulting in the LZW variant that became widely used in data compression.
Concept
The algorithm starts with a dictionary of individual characters, each assigned a fixed-length codeword. As the input is read, longer characters are identified and added to the dictionary, allowing the algorithm to replace these sequences with shorter codewords. This process continues, enabling data compression by substituting variable-length strings with fixed-length codes. The dictionary is built and used during both encoding and decoding, allowing for efficient and reversible data compression.
Compression Algorithm

Example of LZW Coding
Here is an example to explain the LZW compression algorithm process. Assume the input that we need to encode is ‘BBAABABAB’. Our goal is to encode the entire input to the corresponding output using the dictionary. We will read the input character by character as highlighted. The explanation of the algorithm will proceed line by line as highlighted, repeatedly, until the entire input is processed.
We will track the values of each variable in the ‘Variables’ frame, update the dictionary with each new pattern of character or string in the ‘Dictionary’ frame, and display the resulting encoded output in the ‘Output’ frame.
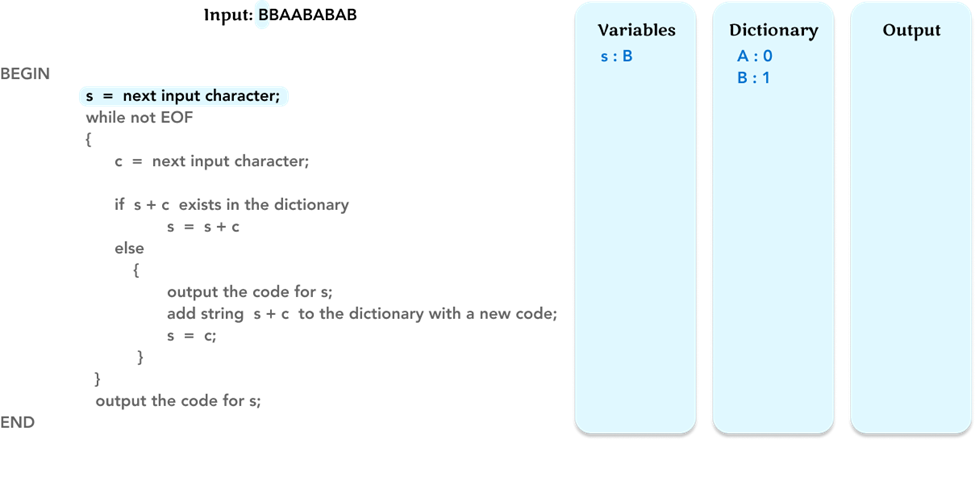
We begin by initializing a dictionary for our encoding process with the initial entries: the character ‘A’ is assigned the code 0, and the character ‘B’ is assigned the code 1. This dictionary is the foundation for building more complex codes as the input is processed.
Next, the first line of the algorithm reads the input’s first character ‘B’, then the character ‘B’ is assigned to the variable ‘s’. Update the value of the variable s in the ‘Variables’ frame.
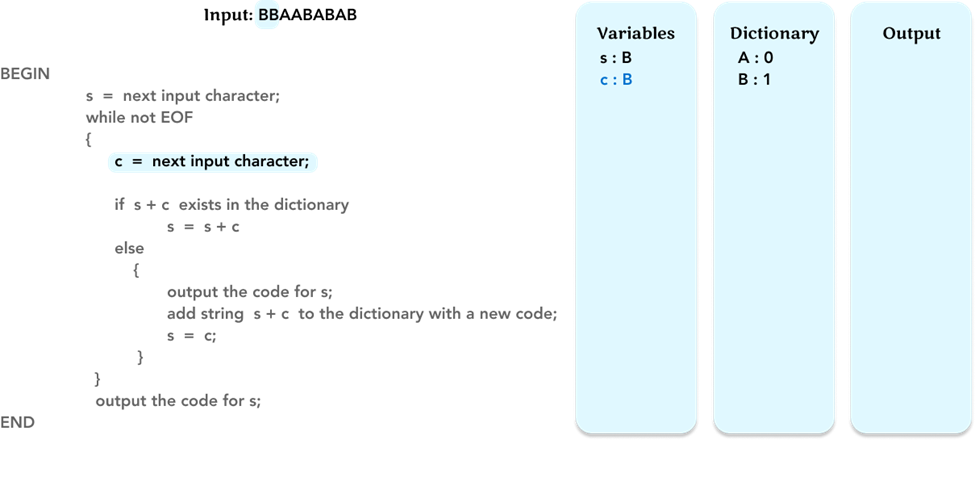
Then we get into the while loop. The next input character ‘B’ (the second character in the input) is assigned to the variable ‘c’. Update the value of variable c in the ‘Variables’ frame.
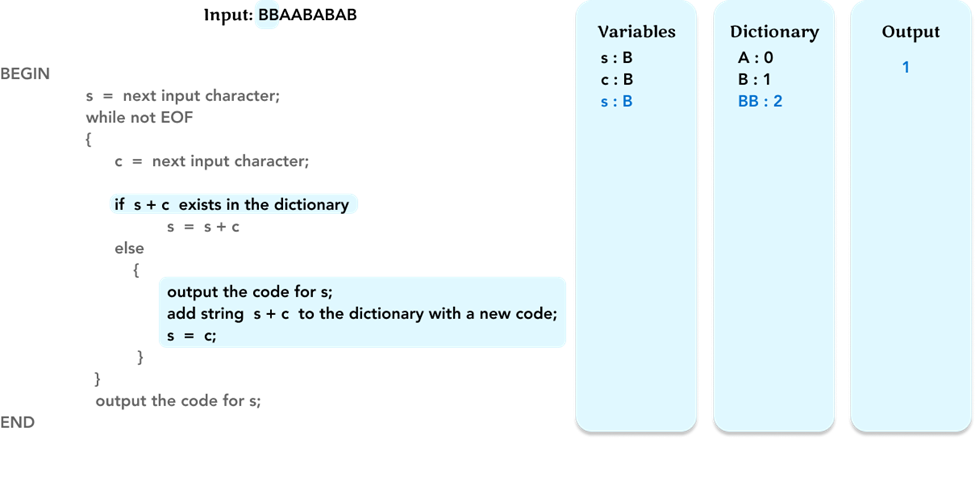
Now we need to check if s + c, ‘BB’, is already in the dictionary, so we go to the ‘Dictionary’ frame and find it just has ‘A’ and ‘B’ initially. Therefore, ‘BB’ is not in the dictionary, the algorithm will jump to the else statements.
First, output the code for s, which is ‘B’. We check the dictionary and find the code of ‘B’ is ‘1’. Therefore, output ‘1’ to the ‘Output’ frame.
Secondly, we find a new pattern, ‘BB’, not in the dictionary, so we add this new pattern ‘BB’ to the ‘Dictionary’ frame with the new code ‘2’.
Thirdly, update the variable value of s. Assign the variable s to the value of c, which is ‘B’. Update the value of the variable s in the ‘Variables’ frame.
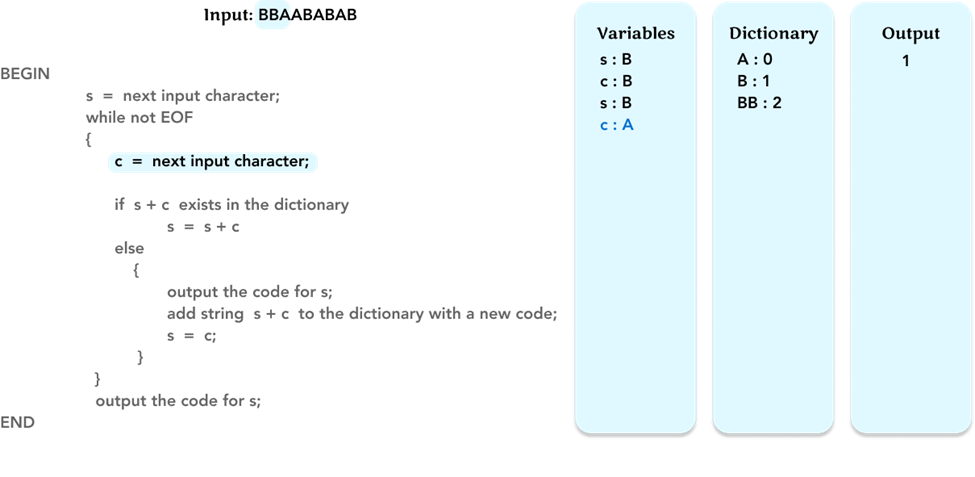
Then we repeat the algorithm in the while loop. As before, read the next character and update the value of variable c in the ‘Variables’ frame.
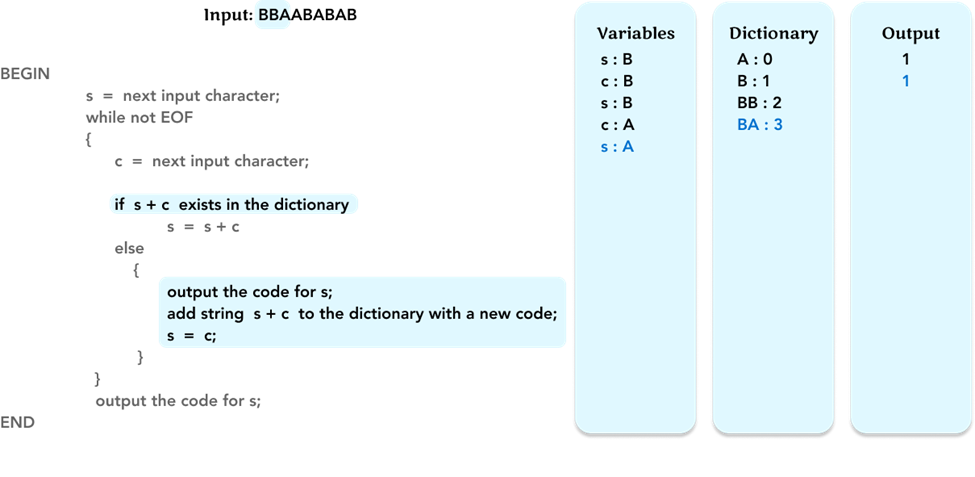
Check if string s + c, ‘BA’, is in the ‘Dictionary’ frame. If not, as before, check the corresponding code of the variable s (= ‘B’) in the dictionary, and output the code ‘1’ for the character ‘B’.
Add string s + c, ‘BA’, as a new pattern to the ‘Dictionary’ frame with new code ‘3’.
Update the value of the variable s to the value of c (= ‘A’).
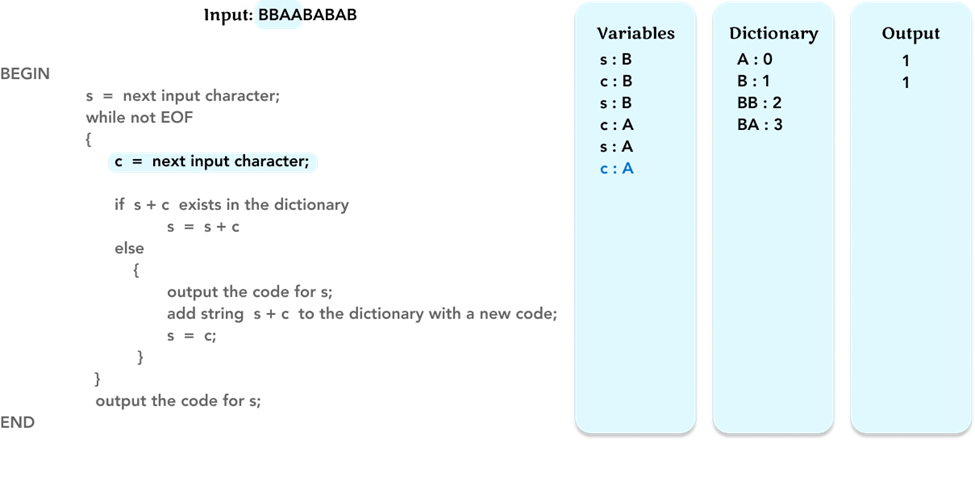
Repeat the algorithm, and update the value of the variable c to the next character ‘A’.
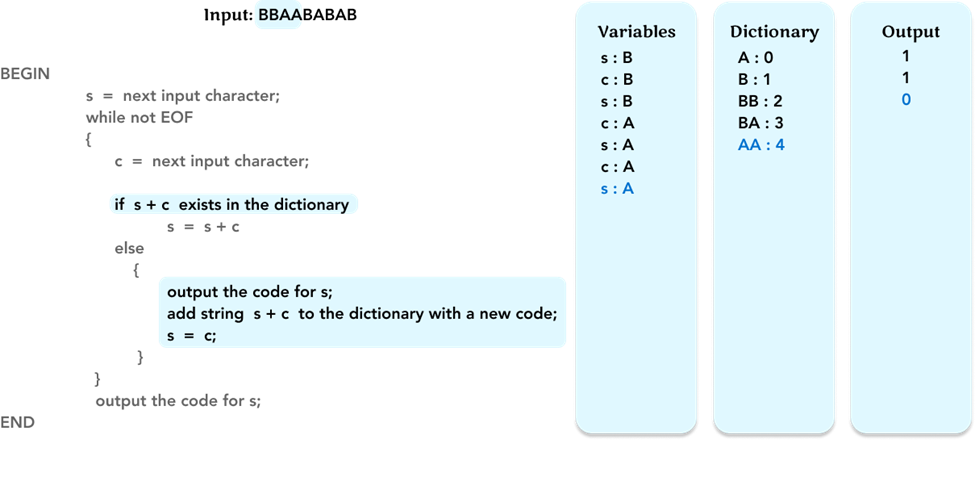
As before, check if string s + c, ‘AA’, is in the dictionary. If not, output the code ‘0’ for s (= ‘A’). Add string ‘AA’ to the dictionary with code ‘4’. Update the value of s to the value of c (= ‘A’).
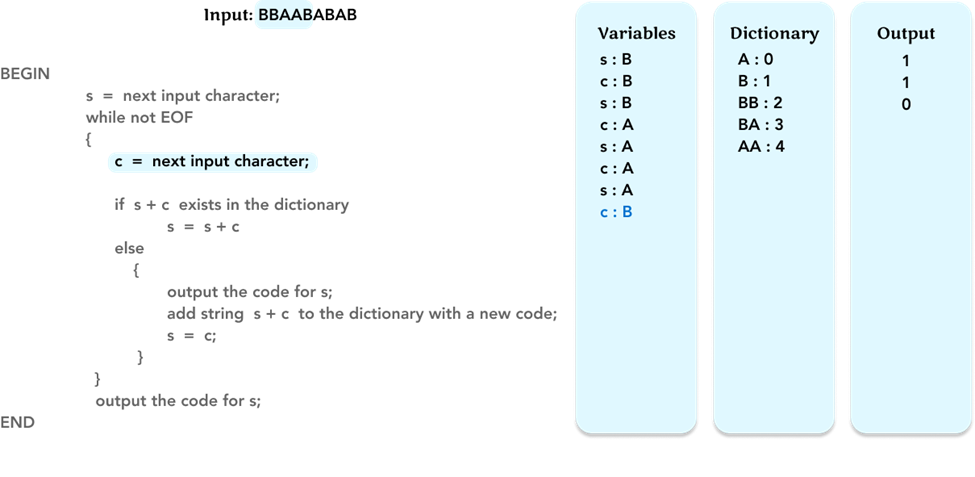
Repeat the algorithm, and update the value of the variable c to the next character ‘B’.
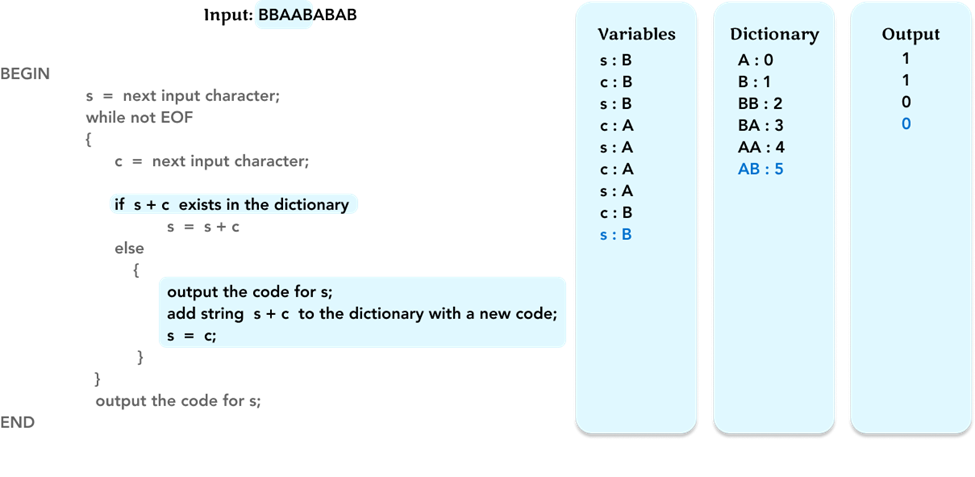
As before, check if string s + c, ‘AB’, is in the dictionary. If not, output the code ‘0’ for s (= ‘A’). Add string ‘AB’ to the dictionary with code ‘5’. Update the value of s to the value of c (= ‘B’).
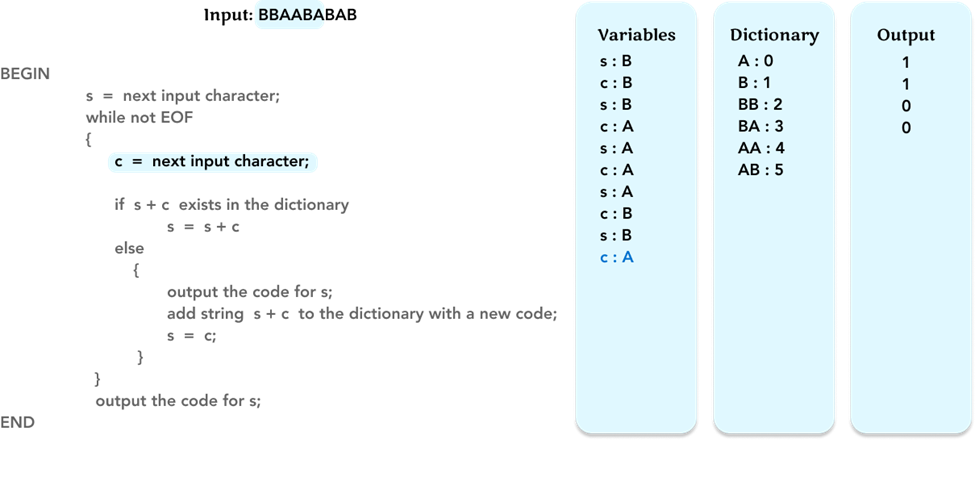
Repeat the algorithm, and update the value of the variable c to the next character ‘A’.
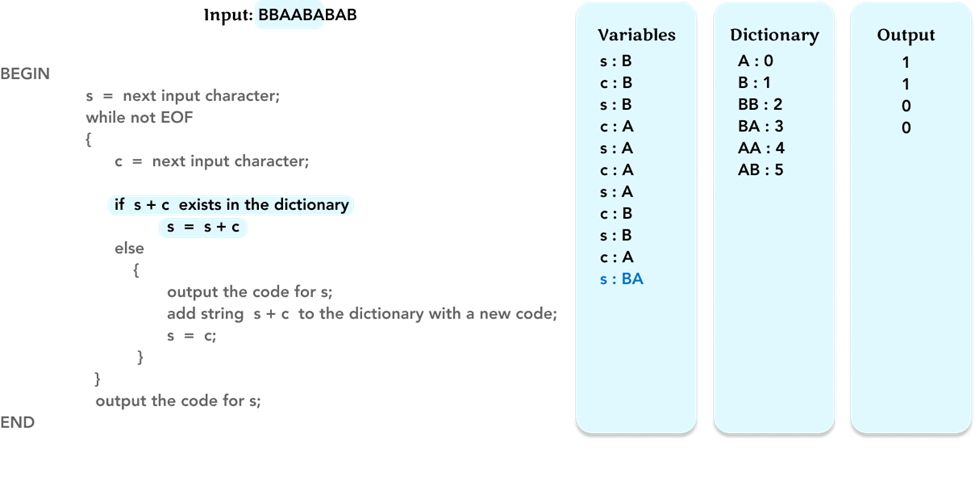
Check if string s + c, ‘BA’, is in the dictionary. We find the ‘BA’ pattern is already in the dictionary. At this step, we do not output the code for s because we want to see if there is any new pattern that starts with ‘BA’. Therefore, we just update the value of the variable s to the value ‘BA’. Then update to the ‘Variables’ frame.
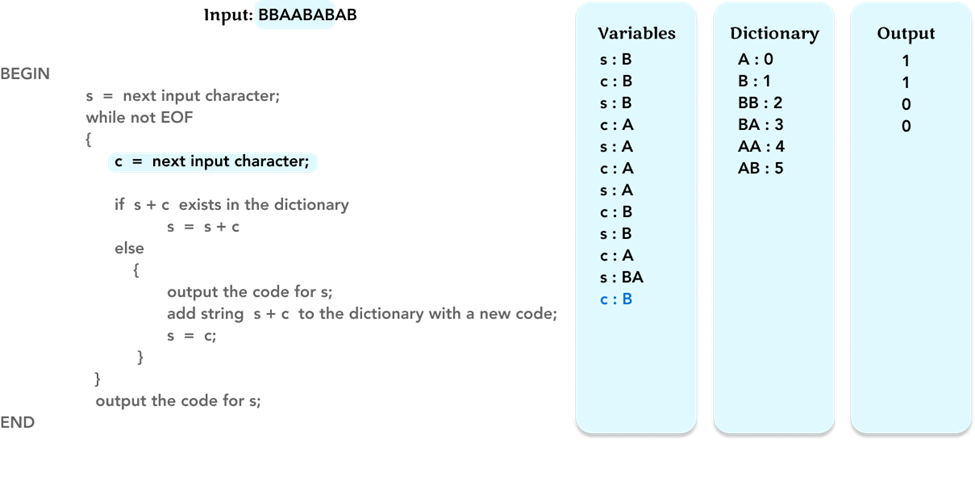
Repeat the algorithm, and update the value of the variable c to the next character ‘B’.
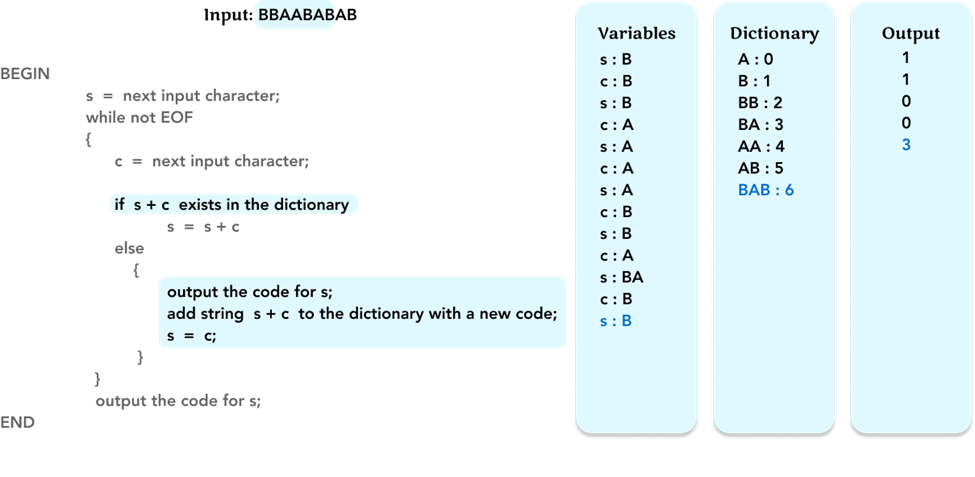
As before, check if string s + c, ‘BAB’, is in the dictionary. If not, output the code ‘3’ for s (= ‘BA’). Add string ‘BAB’ to the dictionary with code ‘6’. Update the value of s to the value of c (= ‘B’).
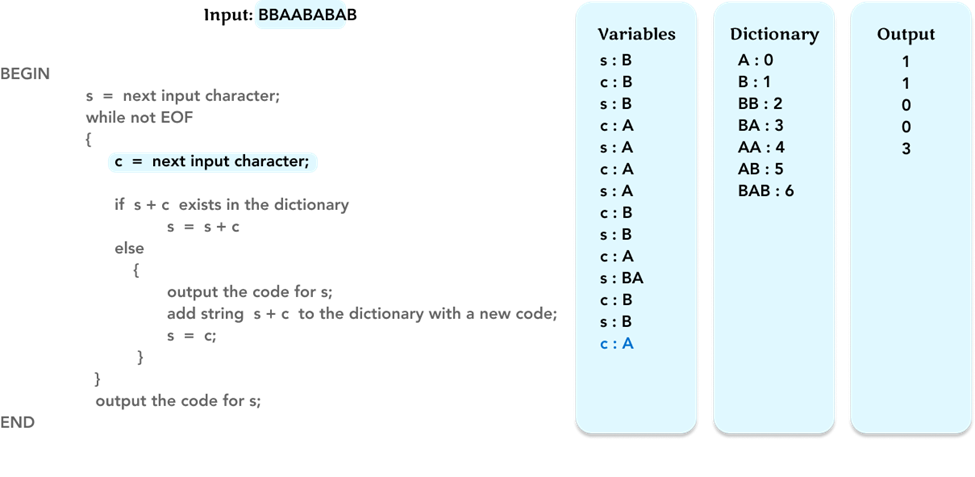
Repeat the algorithm, and update the value of the variable c to the next character ‘A’.
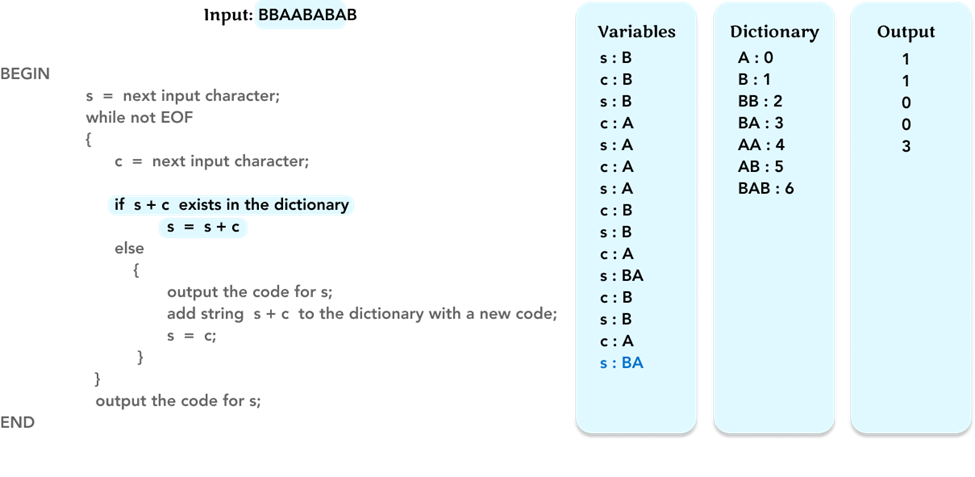
As before, check if string s + c, ‘BA’, is in the dictionary. If yes, we just update the value of the variable of s to the string ‘BA’.
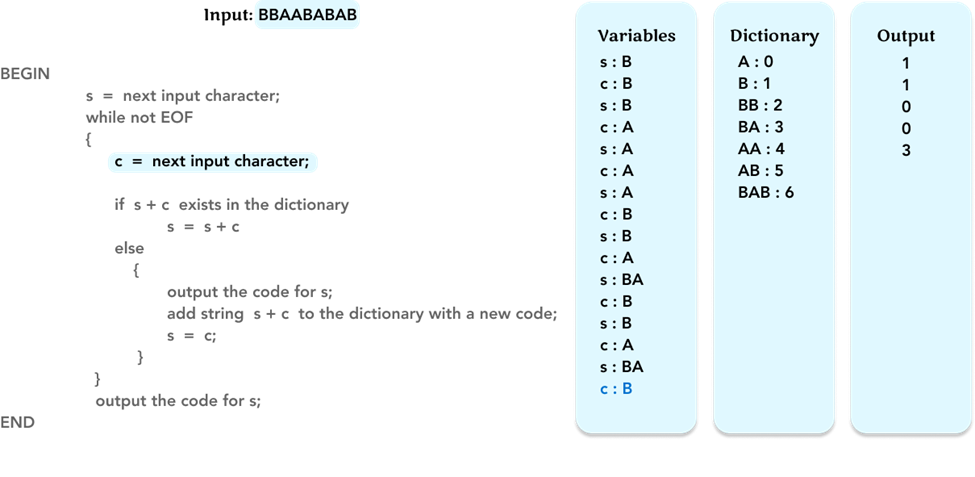
Repeat the algorithm, and update the value of the variable c to the next character ‘B’.
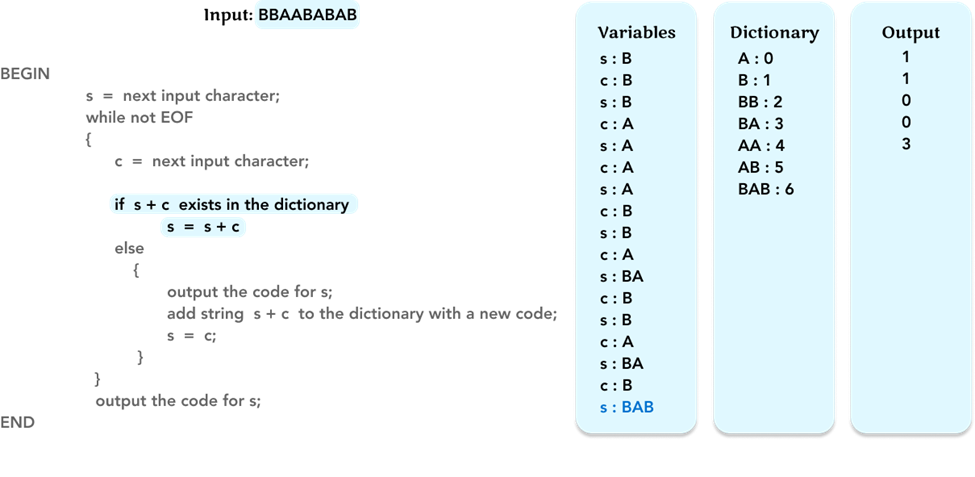
As before, check if string s + c, ‘BAB’, is in the dictionary. If yes, we just update the value of the variable of s to the string ‘BAB’.
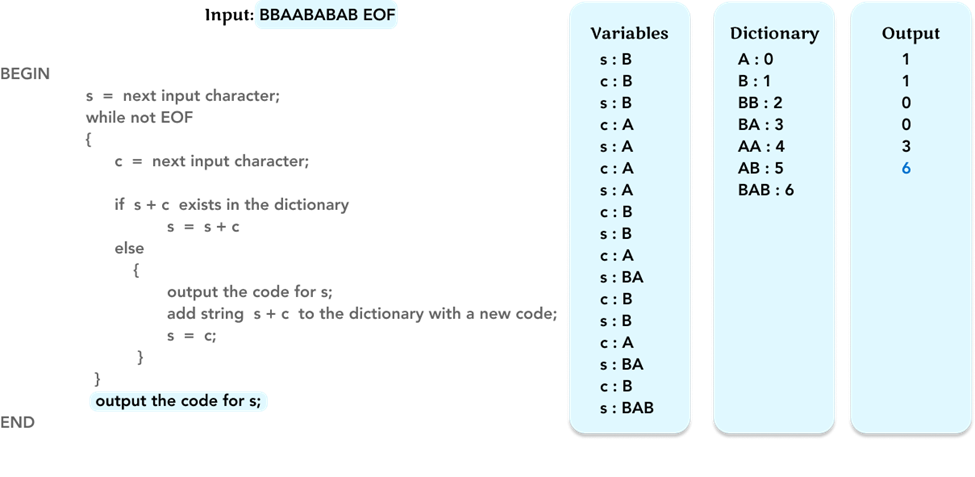
Jump back to the while loop, but this time we have already read all the characters in the input, so we will encounter EOF which means there are no more characters to read in the input. Therefore, we jump out of the while loop and output the code ‘6’ for the variable s (= ‘BAB’).
Each code in the ‘Dictionary’ is 3 bits, because there are 7 entries, we should use 3 bits to represent 2^3 = 8 entries, which covers all the 7 entries in the ‘Dictionary’. There are 6 codes in the output, so the total number of bits to encode the input is 6 * 3 = 18 bits.
Advantages of LZW Coding
The sender does not need to send the entire dictionary to the receiver, it just needs to send the initial dictionary to the receiver before the compression algorithm. The encoder and decoder build up the same dictionary dynamically. In the above example, the sender and receiver build on the initial dictionary with A: 0 and B: 1.
The dictionary grows as the input string is processed, allowing the algorithm to encode longer and longer sequences with fixed-length codewords, leading to better and better compression. It is especially effective for commonly occurring sequences. We can use one fixed-length codeword to represent a longer repeated entry. In the above example, the sequences ‘A’ to ‘BAB’ are longer and longer, but all of these sequences use 3 bits to be encoded.
If using ASCII code (8 bits per character) without the LZW compression algorithm, we need 9 * 8 = 72 bits to encode 9 characters from input. Therefore, LZW compression indeed uses fewer bits to achieve better encoding.

