Simulating brightness levels – Why we use dithering
- Software and hardware: each pixel in a grayscale image varies in intensity. From 0 to 255 for example.
- Hardware (physical) limitation: There are some display mediums (some printers or screens) that can only display a pixel as being either on or off; brightness levels cannot be shown
- We can use dithering to simulate varying pixel brightnesses by replacing them with different concentrations of black dots. The more dense or closer together the black dots are, the more that area of the image seems darker
- Dithering in general actually extends much deeper than what’s discussed in CMPT 365. This concept and basic application is just to build a foundation.
Dithering
Given a grayscale image, we want to replace each pixel with a set of dither pixels. For example: given a 2×2 dither matrix (4 elements) and a 3×3 pixel image (9 elements), our dithered output would be a 6×6 (36 elements) pixel image. Another example: given a 3×3 (9 elements) dither matrix and an 8×8 (64 elements) pixel image, the dithered output would be a 24×24 (576 elements) pixel image.
Ordered Dithering
Ordered dithering is similar to regular dithering except that we do not increase the size of the original image. So the number of output pixels after dithering is the same as the number of pixels in the original image. To keep the output size the same, we “slide” the dither matrix across the pixel image and only compare a single pixel to a single element of the dither matrix.
Dithering Steps
1. Given a dither matrix, we need to first find the number of “bins” to normalize our pixel values to.
This is the number of elements in a dither matrix + 1. This 2×2 dither matrix has 4 elements, so we will have 4 + 1 bins.
| 0 | 2 |
| 1 | 3 |
Now we evenly distribute our image’s value ranges between the 5 bins. For this example our image is 8 bit grayscale, so there are 256 possible pixel values (0-255). 256/5 = 51.2 where 51.2 will be the bin width.
Bin 0 ∈ [0, 51.2]
Bin 1 ∈ (51.2, 102.4]
Bin 2 ∈ (102.4, 153.6]
Bin 3 ∈ (153.6, 204.8]
Bin 4 ∈ (204.8, 255]
We will now replace each pixel value with its corresponding bin number. An example 6×4 pixel image:
Original image
| 0 | 255 | 204 | 205 | 102 | 1 |
| 0 | 253 | 0 | 255 | 154 | 153 |
| 0 | 166 | 0 | 0 | 103 | 102 |
| 0 | 72 | 0 | 0 | 51 | 52 |
Normalized image based on the 2×2 dither matrix
| 0 | 4 | 3 | 4 | 1 | 0 |
| 0 | 4 | 0 | 4 | 3 | 2 |
| 0 | 3 | 0 | 0 | 2 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 |
2. Now for each normalized pixel, we replace it with a 2×2 matrix following this rule: if the pixel value is greater than the element in the dither matrix, it is 1/ON/black. Otherwise it is 0/OFF/white.
For example: a normalized pixel value of 1:
Dither matrix from before
| 0 | 2 |
| 1 | 3 |
After applying dither matrix comparison
| 1 | 0 |
| 0 | 0 |
Another example: a normalized pixel value of 3:
After dither matrix comparison
| 1 | 1 |
| 1 | 0 |
After applying to all pixels, our original image has increased by a factor of the dither matrix’s size. This would be the final output:
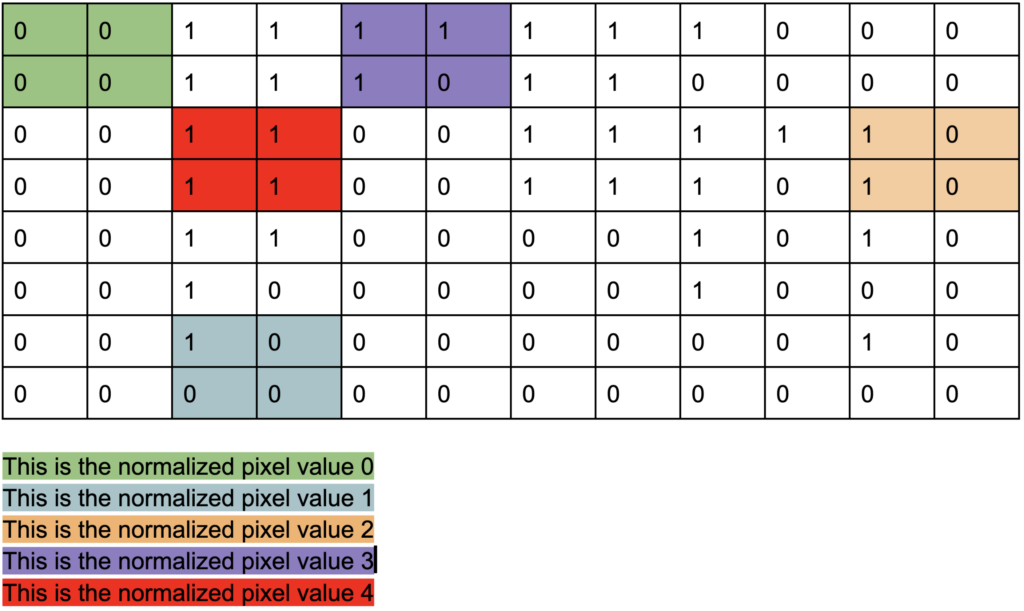
Ordered Dithering Steps
1. Like with dithering, we will normalize the pixel values the exact same way.
Dither matrix
| 0 | 2 |
| 1 | 3 |
Original image (same as previous example)
| 0 | 255 | 204 | 205 | 102 | 1 |
| 0 | 253 | 0 | 255 | 154 | 153 |
| 0 | 166 | 0 | 0 | 103 | 102 |
| 0 | 72 | 0 | 0 | 51 | 52 |
Normalized image based on the 2×2 dither matrix
| 0 | 4 | 3 | 4 | 1 | 0 |
| 0 | 4 | 0 | 4 | 3 | 2 |
| 0 | 3 | 0 | 0 | 2 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 |
2. Compare the dither matrix with the same number of elements from the normalized image. If the normalized pixel is greater than the dither matrix element it is 1/ON/black. Otherwise it is 0/OFF/white.
Let’s look at the first comparison:
Looking at the elements in yellow because our dither matrix is 2×2
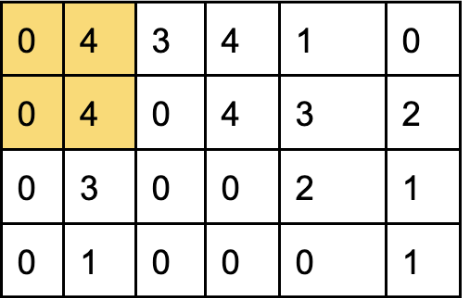
Dither matrix
| 0 | 2 |
| 1 | 3 |
Output for this first section:
Element (0,0) – 0 (normalized matrix) is not greater than 0 (dither matrix). Output 0
Element (0,1) – 0 (normalized matrix) is not greater than 1 (dither matrix). Output 0
Element (1,0) – 4 (normalized matrix) is greater than 2 (dither matrix). Output 1
Element (1,1) – 4 (normalized matrix) is not greater than 3 (dither matrix). Output 1
| 0 | 1 |
| 0 | 1 |
The next comparison:
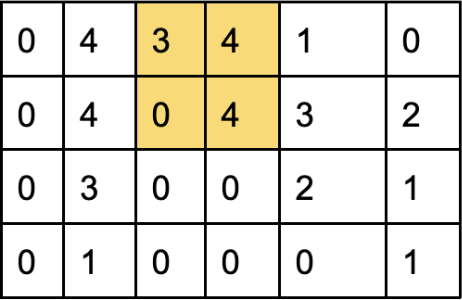
Output for this second section:
Element (0,0) – 3 (normalized matrix) is greater than 0 (dither matrix). Output 1
Element (0,1) – 0 (normalized matrix) is not greater than 1 (dither matrix). Output 0
Element (1,0) – 4 (normalized matrix) is greater than 2 (dither matrix). Output 1
Element (1,1) – 4 (normalized matrix) is not greater than 3 (dither matrix). Output 1
| 1 | 1 |
| 0 | 1 |
Third comparison
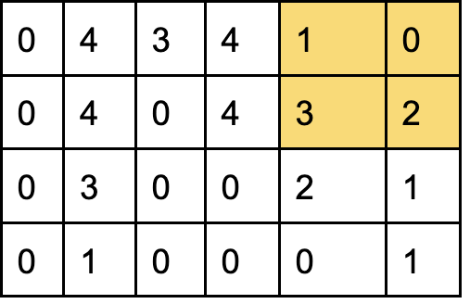
Output:
| 1 | 0 |
| 1 | 0 |
3. Continue sliding the dither matrix to the right until reaching the end, then move down to the next row and repeat. Each image pixel is only compared once with a dither matrix element.
Since we already compared everything element in the first 2 rows, our dither matrix slides to start on row 3
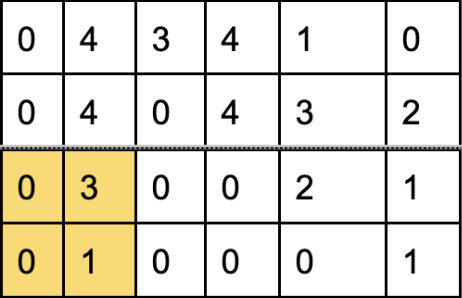
Output:
| 0 | 1 |
| 0 | 0 |
After sliding the dither matrix across our image, this is the final output:
| 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 |
3.5 It’s not always guaranteed that the dither matrix will be a multiple of the dimensions of the image. If the dither matrix does not perfectly overlap the image at its right or bottom edges, we can choose to compare just a portion of the dither matrix to the edge
Eg: the red is where we could potentially do a comparison with just a portion of the dither matrix
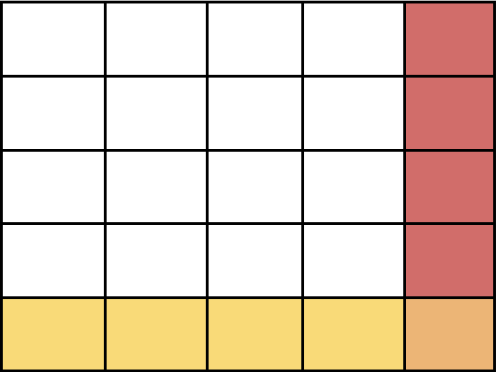
Compares with

or

And the same with the bottom edge.
or

Another example:
Image matrix
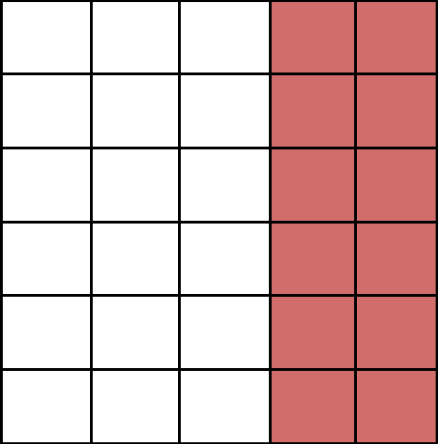
Dither matrix

or

Thinking furhter questions
Does a larger dithering matrix mean more grayscale levels can be displayed?
Do dither matrices need to be an n x n square matrix?
Can a dither matrix have repeating values?
| 0 | 1 |
| 0 | 2 |
Eg:
Given a color image, is dithering still possible? What would be the result?

